[转]深度学习自动编码器如何有效应对维数灾难

From http://blog.sina.com.cn/s/blog_594168770102whsu.html

Deep Learning, The Curse of Dimensionality, and Autoencoders

From http://www.kdnuggets.com/2015/03/deep-learning-curse-dimensionality-autoencoders.html/

Autoencoders are an extremely exciting new approach to unsupervised learning and for many machine learning tasks they have already surpassed the decades of progress made by researchers handpicking features.

对许多机器学习研究者来说，自动编码(Autoencoders)是一个非常激动人心的无监督学习方法，他们取得的进展已经超过了数十年的研究人员研究的手选编码特征。

Let's say you're working on a cool image processing project, and your goal is to build an algorithm that analyzes faces for emotions. It takes in a 256 pixel by 256 pixel greyscale image as its input and spits out an emotion as an answer. For example, if you passed in the following image, you'd expect the algorithm to label it as "happy."

　　假设您正在处理一个很酷的图像处理项目，和你的目标是建立一个算法，分析当时的情感。在256×256像素灰度图像作为输入，然后输出了一个表情作为结果。例如，如果你通过下面的图片,你期望算法的标签是“快乐”。

Now this is all well and good, but before we're satisfied with this approach, let's take a step back and think about what this really means. A 256 by 256 greyscale image corresponds to an input vector of over 65,000 dimensions! In other words, we're trying to solve a problem in a 65,000-dimensional space. That's not a particularly easy thing to do, even for a computer! Not only are large inputs annoying to store, move around, and compute with, but they also give rise to some pretty serious tractability concerns.

在我们满意这种方法之前这看起来非常不错，但是让我们退一步想想这到底意味着什么。256×256像素灰度图像对应一个输入矢量的65000尺寸。换句话说，我们正在试图解决一个在65000维空间的问题。这不是一件特别容易的事,即使对一个电脑来说。不仅是大型输入，存储，移动和计算，而且也产生一些相当不容易处理的干扰。

Dimensionality is Exponentially Worse

Let's get a rough idea of how the difficulty of a machine learning problem increases as the dimensionality increases. According to a study by C.J. Stone in 1982, the time it takes to fit a model (specifically a nonparametric regression) to your data is at best proportional to m^{-p/(2p+d)}, where m is the number of data points, d is the dimensionality of the data, and p is a parameter that depends on the model we are using (specifically, we are assuming that the regression function is p times differentiable). In a nutshell, this relation implies that we need exponentially more training examples was we increase the dimensionality of our inputs.

　　让我们大致了解一下随着维数的增加导致机器学习问题的难度。根据C.J. Stone 在1982年的一项研究显示，所花费的时间(特别是非参数回归)模型适合您的数据在最佳比例是m ^ { – p /(2 p + d)}，m是数据点的数量，数据的维数d,p是一个参数，取决于模型我们使用(具体地说，我们假定回归函数p次可微的)。简而言之，这个关系意味着我们需要更多的训练例子成倍地增加我们的输入维数。

We can observe this graphically by considering a simple example, borrowed from Gutierrez-Osuna. Our learning algorithm divides the feature space uniformly into bins and plot all of our training examples. We then assign each bin a label based on the predominant class that's found in that bin. Finally, for each new example that we want to classify, we just need to figure out the bin the example falls into and the label associated with that bin!

　　通过考虑Gutierrez-Osuna所研究的一个简单的例子我们可以观察这个图形。我们的学习算法将划分特征空间统一进入一个箱子作为我们所有的训练示例。然后我们在每个箱子中分配一个标签根据在箱子中找到的主类。最后,对于每一个我们要分类的新样本，我们只需要找出落入的标签样本和原来的标签。

In our toy problem, we begin by choosing a single feature (one-dimensional inputs) and divide the space into 3 simple bins:

　　在我们的问题中，我们首先选择一个单一特征(一维输入)并把空间分成3个简单的箱子，如下图： Understandably, we notice there's too much overlap between classes, so we decide to add another feature to improve separability. But we notice that if we keep the same number of samples, we get a 2D scatter plot that's really sparse, and it's really hard to ascertain any meaningful relationships without increasing the number of samples. If we move onto 3-dimensional inputs, it becomes even worse. Now we're trying to fill even more 3^{3} = 27 bins with the same number of examples. The scatter plot is nearly empty!

　　可以理解的是，我们注意到有太多的重叠类，所以我们决定添加另一个特性来提高分离性。但是我们注意到，如果我们保持相同数量的样本，我们得到一个二维散点图这真的看起来是非常稀疏的，也真的很难确定任何有意义的关系如**果不增加样本的数量。如果我们进行三维输入，那么它会变得更糟。现在我们试图填补更多3 ^ { 3 } = 27箱与相同数量的例子。散点图几乎是空白。

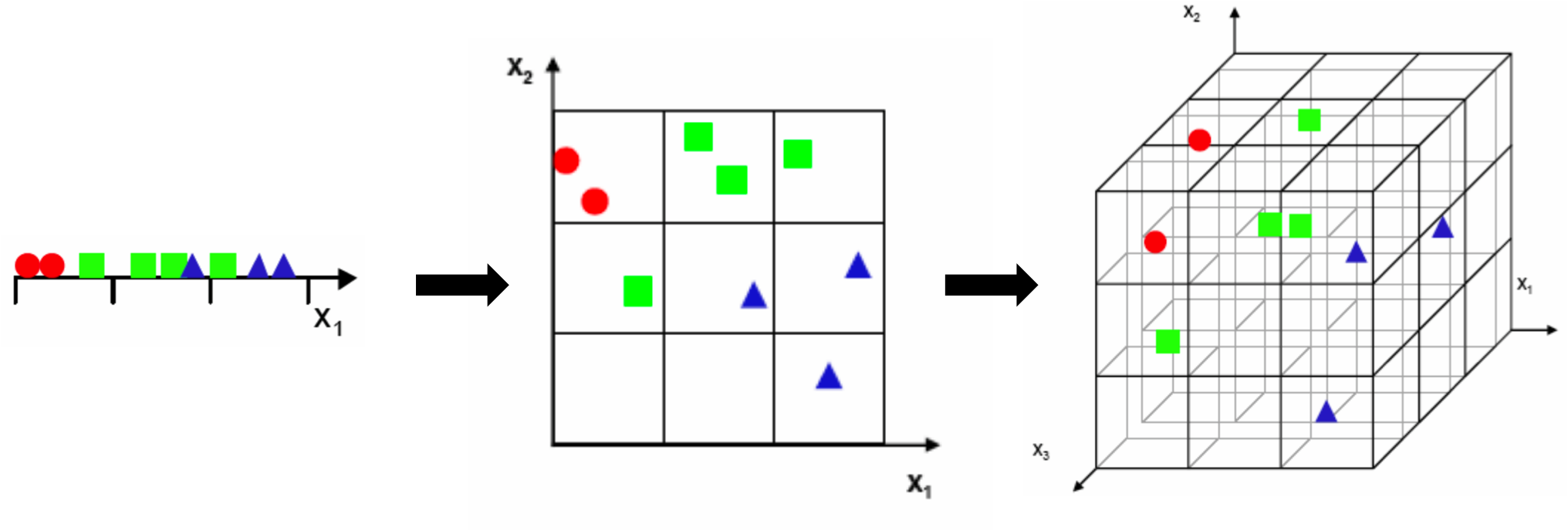
Sparsity becomes exponentially worse as dimension increases

Of important note is that this is NOT an issue that can be easily solved by more effective computing or improved hardware! For many machine learning tasks, collecting training examples is the most time consuming part, so this mathematical result forces us to be careful about the dimensions we choose to analyze. If we are able to express our inputs in few enough dimensions, we might be able to turn an unfeasible problem into a feasible one!

重要的是，这不是一个很容易地可以通过更有效的计算或改善硬件来解决的问题。对许多机器学习者来说，收集培训样本是最耗时的部分，所以这结果迫使我们要谨慎选择分析。如果我们能够输入一些足够小的维度，也许我们可以把一个不可行的问题变成一个可行的问题。

Manual Feature Selection

Going back to the original problem of classifying facial expressions, it's quite clear that we don't need all 65,000 dimensions to classify an image. Specifically, there are certain key features that our brain automatically uses to detect emotion quickly. For example, the curve of the person's lips, the extent his brow is furrowed, and the shape of his eyes all help us determine that the man in the picture is feeling happy. It turns out that these features can be conveniently summarized by looking at the relative positioning of various facial keypoints, and the distances between them.

　　回到最初的判别的面部表情问题，很明显我们不需要65000维度对一个图像进行分类。具体地说，我们的大脑会自动快速地通过有一些关键特征检测情感。例如,人的嘴唇的曲线，在一定程度上的额头上出现了皱纹，和他的眼睛的形状都能帮助我们确定照片中的人是否“快乐”。事实证明，这些特征可以方便地通过观察总结各种面部的相对定位要点、以及它们之间的距离。

Obviously, this allows us to significantly reduce the dimensionality of our input (from 65,000 to about 60), but there are some limitations! Hand selection of features can take years and years of research to optimize. For many problems, the features that matter are not easy to express. For example, it becomes very difficult to select features for generalized object recognition, where the algorithm needs to tell apart birds, from faces, from cars, etc. So how do we extract the most information-rich dimensions from our inputs? This is answered by a field of machine learning that is called unsupervised learning. In the next section, we will be discussing the autoencoder, a unsupervised learning technique pioneered by Geoffrey Hinton that is based on neural networks. We'll briefly talk about how the autoencoder works and how it compares to traditional linear approaches such as principal component analysis (PCA) for computer vision and latent semantic analysis (LSA) for natural language processing.

显然，这允许我们能够显著减少输入的维数(从65000到60)，但也有一些限制。手选择的特征可以年复一年的去研究优化的效果。对于很多问题，特征是不容易选择的。例如，选择广义识别的对象特点这是很难的，算法需要分辨从面孔，从汽车等等。那么从我们的输入信息维度我们该如何提取？这是机器学习的一个领域，称为无监督学习。在下一节中，我们将讨论自动编码（autoencoder），杰弗里?辛顿开创的基于神经网络的一种无监督学习技术。我们将简要讨论自动编码（autoencoder）是如何工作并且如何与传统的线性方法的差距。例如对计算机视觉的主成分分析(PCA)和潜在语义分析(LSA)的自然语言处理。

自动编码（Autoencoder）的简要概述

A Brief Overview of the Autoencoder

An autoencoder is an unsupervised machine learning technique that utilizes a neural network to produce a low dimensional representation of a high dimensional input. Traditionally, dimensionality reduction depended on linear methods such as PCA, which finds the directions of maximal variance in high-dimensional data. By selecting only those axes that have the largest variance, PCA aims to capture the directions that contain the most information about the inputs, so we can express as much as possible with a minimal number of dimensions. The linearity of PCA, however, places significant limitations on the kinds of feature dimensions that can be extracted. Autoencoders overcome these limitations by exploiting the inherent nonlinearity of neural networks.

　自动编码（autoencoder）是一种无监督的机器学习技术，利用神经网络产生的低维来代表高维输入。传统上，依靠线性降维方法，如主成分分析（PCA），找到最大方差在高维数据的方向。通过选择只有那些有最大方差的轴，主成分分析（PCA）的目的是捕获包含的大部分信息输入的方向，所以我们可以尽可能用最小数量的维度。主成分分析（PCA）的线性度然而限制了可以提取的特征维度。但是自动编码（Autoencoders）用固有的非线性神经网络克服了这些限制。

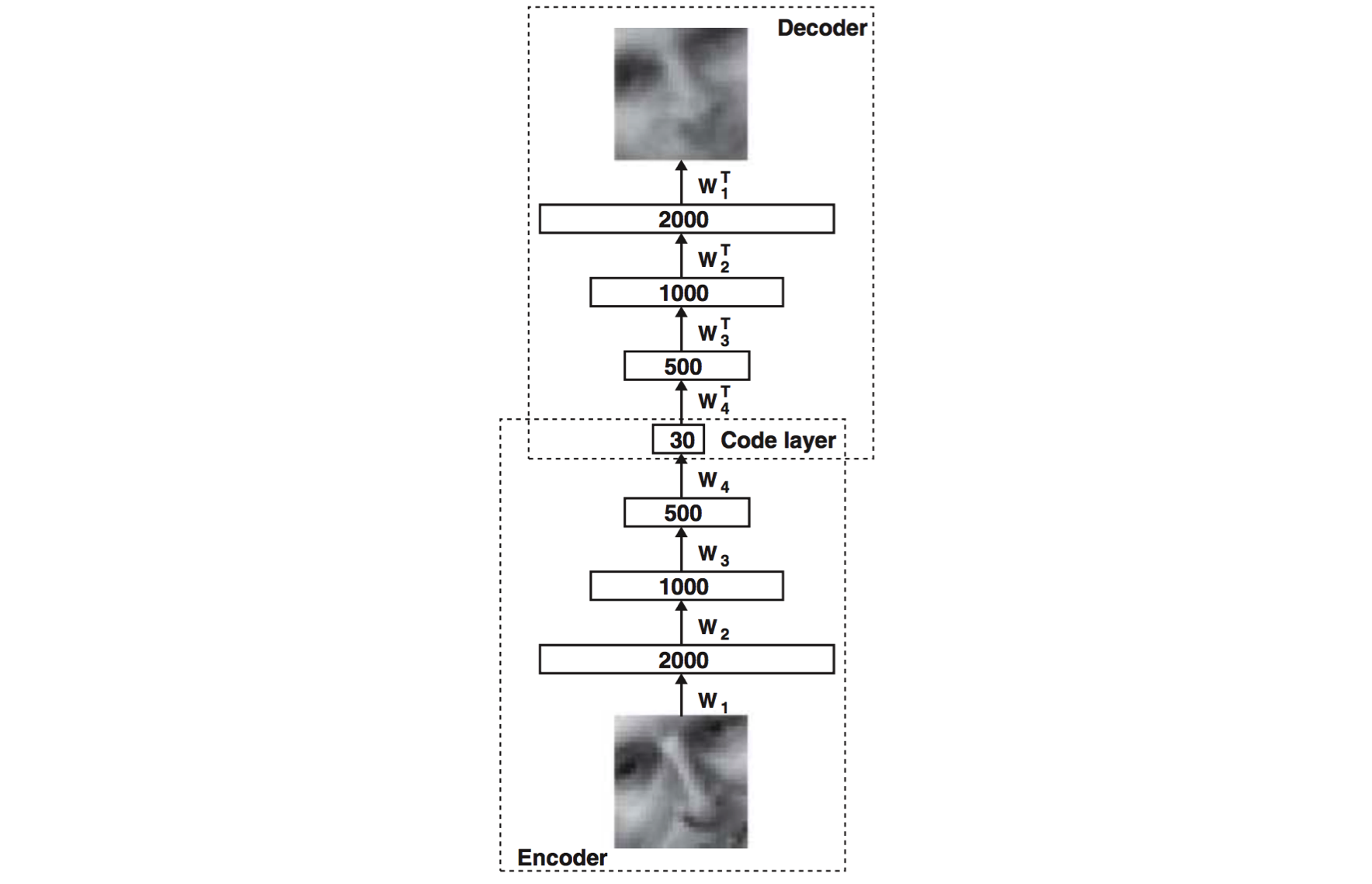
自动编码（autoencoder）的基本结构

An autoencoder consists of two major parts, the encoder and the decoder networks. The encoder network is used during both training and deployment, while the decoder network is only used during training. The purpose of the encoder network is to discover a compressed representation of the given input. In this example, we are generating a 30-dimensional representation from a 2000-dimensional input. The purpose of the decoder network, which is just a reflection of the encoder network, is to reconstruct the original input as closely as possible. It is used during training in order to force the autoencoder to choose the most informative features in its compressed representation. The closer the reconstructed input is to the original, the better our original representation!

自动编码（autoencoder）由两个主要部分组成，编码器网络和译码器网络。编码器网络在训练和部署的时候被使用，而译码器网络只是在训练的时候使用。编码器网络的目的是找到一个给定的输入的压缩表示。在这个例子中，我们从2000 个维度的输入中生成了30个维度。译码器网络的目的只是一个编码器网络的反射，是重建原始输入尽可能密切。使用它在训练的目的是为了迫使自动编码（autoencoder）选择最丰富特征的压缩。尽可能靠近原始输入。

So how does the autoencoder compare to its linear competitors? Let's take a look at a number of experiments performed by Hinton and Salakhutdinov when the technique debuted in 2006. First, we take a look at how well autoencoders can reconstruct their original output compared to PCA using 30 dimensions.

　　所以自动编码（autoencoder）如何与线性竞争对手比较？让我们看看一些由Hinton and Salakhutdinov在2006年首次亮相的实验。首先，,我们看看自动编码（autoencoders）如何可以重建原来的输出与使用30维度主成分分析（PCA）相比。

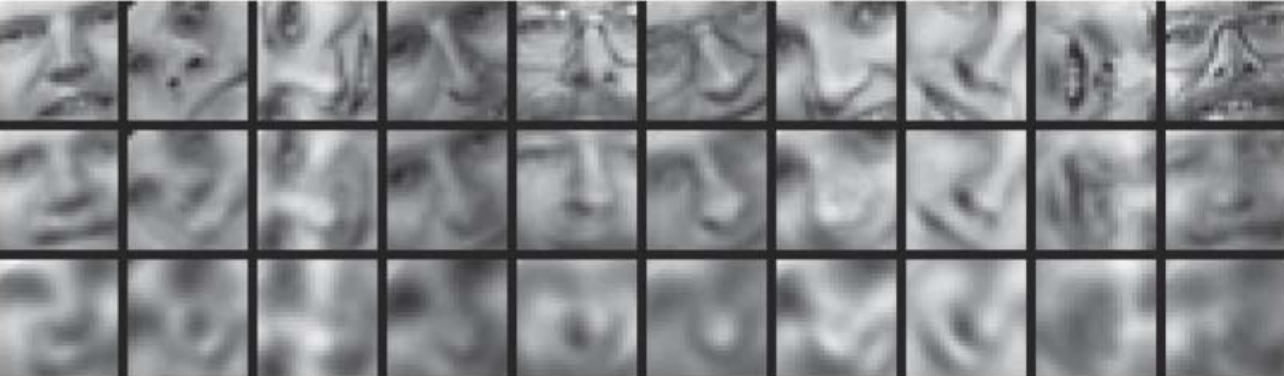自动编码（autoencoder）(中间)和PCA(底部)原始图像输入(上)

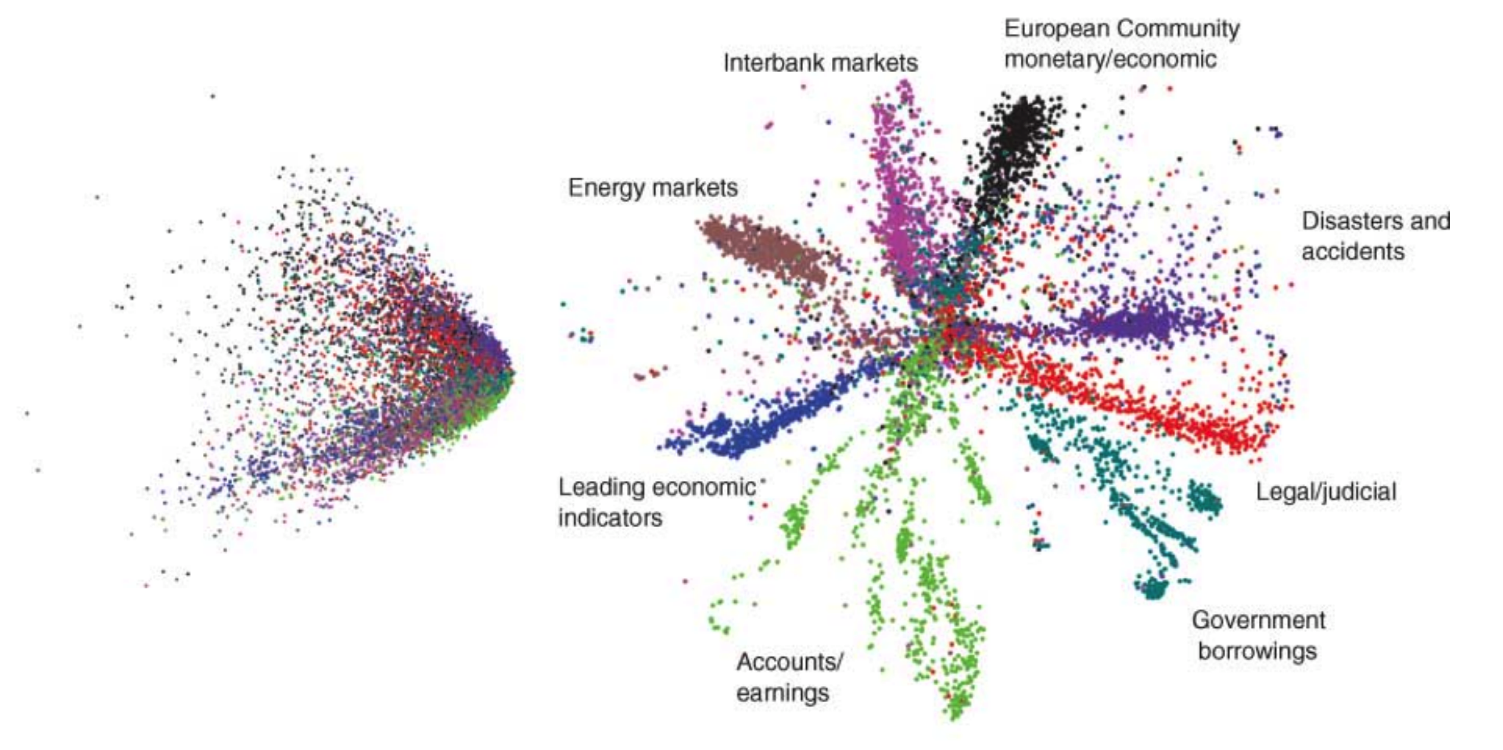
The reconstruction by the autoencoder is visibly better than the PCA output, which is a very promising result. We then explore whether autoencoders can significantly improve the separability of our dataset by comparing 2-dimensional codes produced by an autoencoder to a 2-dimensional representation generated by PCA on the MNIST handwritten digit dataset.

　　从上图可以看出，自动编码（autoencoder）明显优于PCA输出,，这是一个非常理想的结果。我们可以探索自动编码（autoencoders）是否可以显著提高我们的数据集通过比较二维可分性准则。这个由一个二维的自动编码（autoencoder）生成的PCA的数据集。 比较二维可分性的准则生成的自动编码（autoencoder）(右)和PCA(左)数据集

Finally, we see even more drastic improvements when we compare the autoencoder to the gold-standard unsupervised learning technique for natural language (LSA).

　　最后，我们更大幅度的改进，当我们把自动编码（autoencoder）对照无监督学习技术自然语言(LSA)。 结论：

Autoencoders are an extremely exciting new approach to unsupervised learning, and for virtually every major kind of machine learning task, they have already surpassed the decades of progress made by researchers handpicking features! We've covered a lot of ground, but we're still only at the tip of the iceberg. In the next blog post, I'll go into much more depth on how autoencoders work, how we efficiently train them, and other clever optimizations (such as sparsity). If you're interested and would like to talk, please feel free to drop me a line at [email protected]. I'm always excited to hear new perspectives

　　自动编码（Autoencoders）无监督学习对于每一个主要的机器学习任务是一个非常令人兴奋的新方法，他们已经取得的进展超过了数十年的研究人员通过手选特征来研究的进展，我们讨论了很多，但我们仍然只在冰山的一角。在接下来的博客文章，我将进入更深度探讨自动编码（autoencoders）是如何工作的？如何有效地训练他们？和其他有效的优化(如稀疏)。